Background
The EU steel beam calculator can be used to calculate both the demands as well as the resistance of a straight beam.The analysis capabilities include:
- Point transverse forces and point uni-axial moments (excluding torsion)
- Line Loads (including linearly varying)
- Distributed Loads (including varying tributary width). For details on tributary widths, refer article 170-what-is-tributary-width
- Cross Section Classification (Class 4 section design not available)
- ULS: Moment Resistance (EN 1993-1-1:2005 Cl 6.2.5)
- ULS: Shear Resistance (EN 1993-1-1:2005 Cl 6.2.6)
- ULS: Buckling Resistance of Uniform Member in Bending (EN 1993-1-1:2005 Cl 6.3.2)
- ULS: Buckling Resistance of Uniform Member in Shear (EN 1993-1-5:2006 Cl 5.1-5.5) including transverse stiffeners.
- SLS: Deflection analysis
- Penetrations or fastener holes (checks if they may be ignored)
Tutorial
In this worked design example, we will go through the design process of a two-span continuous steel beam. It will be an interior beam, holding a 150mm concrete slab and a regular office live load. The first span is 6m long and the second one is 4m long. Beam spacing is at every 3m feet, and the beam is laterally restrained only at supports.1. Entering our key properties
First, we enter the key properties of our beam:- Member Type & Steel Grade - Clicking “Select” will open a list of all properties and allow you to select an initial size and grade. Refer to related article Quickly finding the best section with the member selector
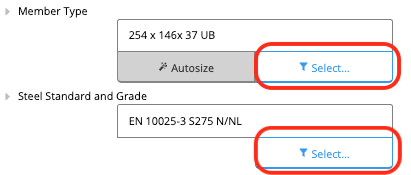
- Total Beam Length - The length between start and end of the beam, irrespective of the support conditions.
- Length between lateral restraints - Let’s conservatively assume that the beam is only braced at supports, so the length between lateral restraints is equal to our maximum beam span of 6m. We can also enter “L_maxspan”, which will always default to the largest span between supports, as shown below:
 Position of Supports from Left - The support conditions may be at any position along the beam. A cantilever can be created on either end by moving the support condition away from “0” or the “Total Beam Length”
Position of Supports from Left - The support conditions may be at any position along the beam. A cantilever can be created on either end by moving the support condition away from “0” or the “Total Beam Length”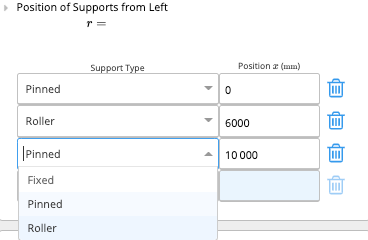
2. Load Details
We enter the tributary width as 3 metres. For dead load, we have a 150mm concrete slab (3.6 kPa for 2400 kg/m3 density) and a 1.2 kPa super-imposed dead load. We can let ClearCalcs calculate the dead load in PSF by entering in the weight of concrete and multiplying by the slab thickness. ClearCalcs will resolve the units and warn you if you are using incorrect units.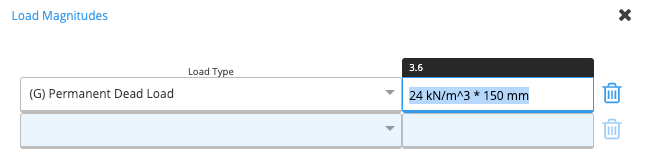 For the office loads we use BS EN1993-1-1:2002 Table 6.2 (For Category B, 2.0kPa to 3.0kPa may be used). For the imposed loads, 1.2 kPa is used for other imposed loads such as tiling or
For the office loads we use BS EN1993-1-1:2002 Table 6.2 (For Category B, 2.0kPa to 3.0kPa may be used). For the imposed loads, 1.2 kPa is used for other imposed loads such as tiling or
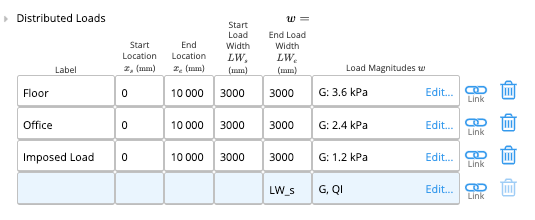 Self-weight may be automatically calculated using the self-weight toggle.
Self-weight may be automatically calculated using the self-weight toggle.
 Now Table 6.2 BS EN1993-1-1:2002 also requires that we apply a 1.5 to 4.5 kN concentrated load for measuring local effects in office spaces. This load doesn’t occur at the same time as the uniformly distributed live load. In this case, it’s pretty clear that it won’t govern, but we will still apply for the example. Since the concentrated load doesn’t apply at the same time as the UDL, we’ll apply it in the “Point & Moment Loads” section.
We apply the loads at the mid-span locations (3000mm and 8000mm). Note how we enter the load type as “L2” in this case. This means that the internal FEA solver will apply “QI” and “QI2” separately, and output the envelope of each case.
Now Table 6.2 BS EN1993-1-1:2002 also requires that we apply a 1.5 to 4.5 kN concentrated load for measuring local effects in office spaces. This load doesn’t occur at the same time as the uniformly distributed live load. In this case, it’s pretty clear that it won’t govern, but we will still apply for the example. Since the concentrated load doesn’t apply at the same time as the UDL, we’ll apply it in the “Point & Moment Loads” section.
We apply the loads at the mid-span locations (3000mm and 8000mm). Note how we enter the load type as “L2” in this case. This means that the internal FEA solver will apply “QI” and “QI2” separately, and output the envelope of each case.
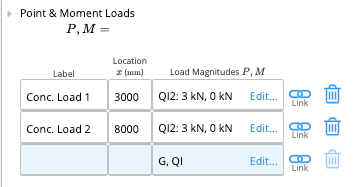 We can now verify that our loads are all properly placed:
We can now verify that our loads are all properly placed:
 Note that the loads shown here are, by default, unfactored under the 1.35G + 1.5Q load combination. The load combination can easily be changed with the dropdown above the graphics.
Note that the loads shown here are, by default, unfactored under the 1.35G + 1.5Q load combination. The load combination can easily be changed with the dropdown above the graphics.
3. Design Criteria
Deflection limits values are to be entered depending upon the national annex and depending upon the use of the structure. In our case, we shall assume the structure is designed according to Table NA.2 BS EN1993-1-1:2014 (UK annex) and carries a plaster ceiling. Therefore, the characteristic load combination due to variable load only is span / 360. The absolute criterion can be adjusted that set a hard limit on any deflections. This may be set project-wide in your Project Defaults or can be manually set for this structure.
The absolute criterion can be adjusted that set a hard limit on any deflections. This may be set project-wide in your Project Defaults or can be manually set for this structure.
4. Section selection
At this point, we are ready to revise our member size. We go back to our “Member Type” tab and search for a utilisation close to but not exceeding 100 %: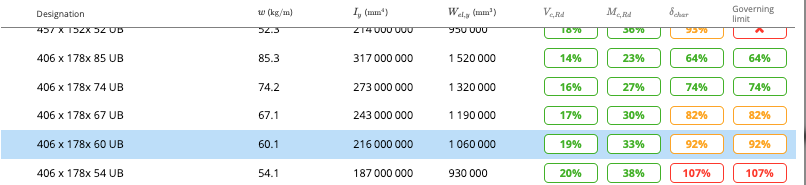 The four right-most columns indicate the utilization for the three governing modes – shear, moment, characteristic deflection, and governing. The governing column considers all checks and validation requirements within the entire calculation. Ideally, we want the minimal weight section that will satisfy all three modes. It is then a matter of scrolling to find the best cross-section. Looking through, we find two candidates – 406 x 178 x 67 UB and 457 x 152 x 60 UB. We pick the shorter section even though it is slightly heavier, so as to reduce the required floor thickness.
That’s it! We’ve now designed our beam!
The four right-most columns indicate the utilization for the three governing modes – shear, moment, characteristic deflection, and governing. The governing column considers all checks and validation requirements within the entire calculation. Ideally, we want the minimal weight section that will satisfy all three modes. It is then a matter of scrolling to find the best cross-section. Looking through, we find two candidates – 406 x 178 x 67 UB and 457 x 152 x 60 UB. We pick the shorter section even though it is slightly heavier, so as to reduce the required floor thickness.
That’s it! We’ve now designed our beam!
5. Summary of results and internal force diagrams
Once we’ve got our beam design, we can quickly glance at relevant values to make sure everything corresponds to what we’d expect. On the right panel is the summary section, where we find things such as the critical moment demand and capacity, shear, moment and deflections. Where a calculation for lateral torsional buckling or web shear buckling was required based on Eurocode criteria, totals will also be shown. We can also look at the shear, bending and deflection diagrams to make sure they correspond to what we anticipate.
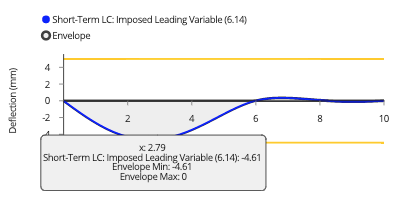
For deflections, we need to switch the load case to reflect a serviceability load case – for here, it is simply “Service CHAR: Imposed Leading Variable”. We can scroll down the graph to see exact deflection values at different points. We clearly see that our deflection is limited by the 5mm hard limit we set. We may need to consider whether that hard limit is in fact required for this specific structure.
We can also look at the shear, bending and deflection diagrams to make sure they correspond to what we anticipate.
For deflections, we need to switch the load case to reflect a serviceability load case – for here, it is simply “Service CHAR: Imposed Leading Variable”. We can scroll down the graph to see exact deflection values at different points. We clearly see that our deflection is limited by the 5mm hard limit we set. We may need to consider whether that hard limit is in fact required for this specific structure.
 A more in-depth look
A more in-depth look
While the previous steps are all that is required to design our beam, it may be desirable to see more information about the beam. ClearCalcs fully exposes all code calculations to see every step of the process employed to design the beam. For instance, we can go look at how the lateral-torsional buckling strength is calculated. Some calculations are hidden for clarity, however, they can be made visible by selecting “Detailed” mode. See 163-how-to-view-all-detailed-calculation-steps. For example, see the equation for the elastic critical buckling moment
 This concludes our short tutorial on designing a steel beam per EN1993-1-1:2015 with ClearCalcs.
This concludes our short tutorial on designing a steel beam per EN1993-1-1:2015 with ClearCalcs.
Assumptions and Limitations
- Beams are computed by a chosen limit state and load combination. It is up to the user to choose limit states to determine the worst loading case combination. These may be viewed and/or modified in Project Defaults.